Закон распределения случайной величины, дисперсия, математическое ожидание..
liliana :
Случайной величиной называется величина, которая в результате опыта может принять то или иное значение, неизвестно заранее, какое именно.
Дискретной случайной величиной называется случайная величина, принимающая отдельные друг от друга значения, которые можно перенумеровать.
Непрерывной случайной величиной называется случайная величина, возможные значения которой непрерывно заполняют какой-то промежуток.
Законом распределения случайной величины называется всякое соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими им вероятностями. Закон распределения может иметь разные формы.
Рядом распределения дискретной случайной величины Х называется таблица, где перечислены возможные (различные) значения этой случайной величины х1, х2, ..., хn с соответствующими им вероятностями р1, р2, ..., рn:
|
хi
|
x1
|
x2
|
...
|
xn
|
|
pi
|
p1
|
p2
|
|
pn
|
Мода дискретной случайной величины Mo(X) - это значение случайной величины, имеющее наибольшую вероятность.
Математическое ожидание вычисляется по формуле:
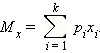
Дисперсия случайной величины вычисляется по формуле: