Подготовка к ЕГЭ по математике. Задания В8. Стереометрия.
liliana :
В Задании B8 предлагается решить простейшие задачи по стереометрии на вычисление площади поверхности или объема многогранника или тела вращения.
Задания ЕГЭ по математике B8 с решениями.
Вычислить объем многогранника.
1. Найдите объем многогранника, изображенного на рисунке
(все двугранные углы многогранника прямые).
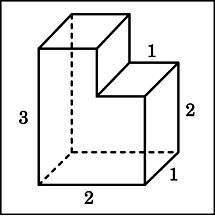 Решение: V1-V2 = 3*2*1 - 1*2*1 = 4
Решение: V1-V2 = 3*2*1 - 1*2*1 = 4
2. Цилиндр и конус имеют общее основание и общую высоту.
Вычислите объем цилиндра, если объем конуса равен 18.
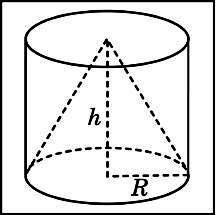
Решение.
Vцилиндра = Sоснования·h; Vконуса = Sоснования·h / 3,
т.е. объём цилиндра в 3 раза больше объёма конуса.
Vцилиндра = 18·3 = 54.