Вопросы»Задачи ЕГЭ по стереометрии с решениями и чертежами. ЕГЭ профильный.|Поступи в ВУЗ

№ 1. Апофема правильной четырехугольной пирамиды SABCD равна 10, радиус окружности, описанной около основания, равен 4. Найдите косинус двугранного угла при основании пирамиды.

Решение.

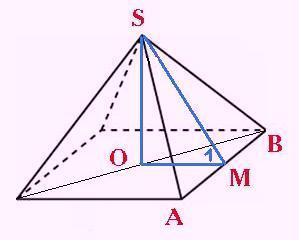
Дано: SM=10; OB=4. В основании квадрат .

Пусть OM=MB=x. x²+x²=OB²; 2х² =16 ; х=2√2

cosOMS = OM/SM = 2√2 /10 = √2/5

liliana

( +3192 ) 06.11.2013 22:28	Комментировать
№ 2. В прямоугольном параллелепипеде АВСDA1B1C1D1 известны ребра AA1=6, AB=6, AD=3√13. Найдите площадь сечения параллелепипеда плоскостью A1MK , где точки M и K разбивают ребра BB1 и CC1 в отношении 1:2 считая от прямой BC. Решение. Рассмотрим 3-к А1NM. AN=x, A1N=2x, A1N=62/3=4 По т. Пифагора: А1М²= NM² + A1N² = 4² + 6² = 52 A1M = 2√13 В сечении получили 4-к А1МКD1 - прямоугольник, т.к. он параллелограмм (А1D1 и МК равны и параллельны) и А1М _\|_ MK по т. о 3-х перпендикулярах. S сеч = МКА1М = 3√13 * 2√13 = 613=78 Ответ: 78*

liliana

( +3192 ) 06.11.2013 23:29	Комментировать
№ 3. Высота правильной четырехугольной призмы равна 8, а сторона основаня 6√2. Найти расстояние от вершины А до плоскости А1ВD. Решение. Т.к. призма правильная, то в основании - квадрат, значит диагонали перпендикулярны. OA _\|_ BD ; OA = AC/2 = BD/2; *В 3-ке DOA: OA² + OD² = DA²; 2x² = 362; OA = x = 6. В 3-ке АОА₁ проведем АК_\|_ОА₁ , АК - расстояние до плоскости А₁BD. A₁O = √(8²+6²) = 10 AKOA₁ = OAAA₁; AK = 68/10 = 4,8.* Ответ: 4,8. № 4. Ребро куба равно 10 см. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины. Решение, В основании призмы - прямоугольный 3-к с катетами 5 и 5. Sосн= 1/2 * 55 = 12,5 Высота призмы равна длине ребра куба = 10. V призмы= 12,510=125 № 5. Площадь основания правильной призмы ABCDA1B1C1D1 равна 0,5 кв.см. Высота призмы равна 9 см. Найдите площадь сечения A1B1CD. Решение. В основании правильной призмы лежит квадрат. Sосн= АВ²=0,5 --> AB=ВС=√0,5 Т.к. грань АА1D1D \| DC, то А1D \| DC --> сечение A1B1CD - прямоугольник. Sсеч=А1DDС. Найдем А1D из 3-ка АА1D по теореме Пифагора. А1D² = АD²+АА1²= (√0,5² + 9²) = 81,5 A1D=√81,5 Sсеч=√(81,5√0,5 =√40,75 ≈6,38

zar_a_zar

24.11.2013 15:35	Комментировать
*Окуда взяли пропорцию AKOA₁ = OAAA чтобы найти АК? Почему АК - расстояние до плоскости, а не ОА*

liliana

( +3192 ) 24.11.2013 20:06	Комментировать
1) Расстояние от точки до плоскости это перпендикуляр. Вы считаете, что ОА _\|_ плоскости A₁BD ? Прямая перпендикулярна плоскости, если она перпендикулярна двум пересекающимся прямым в этой плоскости. 2) В 3-ке А₁АО угол О=90⁰, проводим перпендикуляр АК к гипотенузе. Затем вычисляем площадь этого 3-ка через высоту и гипотенузу и через произведение катетов. И приравниваем.

liliana

( +3192 ) 06.11.2013 23:46	Комментировать
№ 6. В правильной шестиугольной пирамиде сторона основания равна 4√3, а высота равна 8. Найдите апофему пирамиды. Решение. Угол правильного многоугольника равен (n-2)180/n, n - число сторон многоугольника. Угол правильного 6-угольника равен (6-2)180/6 = 120^о Соединим центр шестиугольника О с вершинами одной из сторон, например, АВ. Получим равносторонний треугольник ОАВ со сторонами 4√3 (т.к. ОА делит угол в 120^о пополам). Проведём из О отрезок к середине стороны АВ (точка К). Т.к. треуг АОВ равносторонний, то ОК медиана, биссектриса и высота. Получим прямоугольный треугольник с гипотенузой ОА= 4√3 и катетом АК= 2√3. ОК=√((4√3)²-(2√3)²) = 6 Апофема боковой грани равна SK = √(8²+6²) = 10 Ответ: 10

Хочу написать ответ