liliana :

№ 1.  lim_x→2   (x -2) / (√(3x-2)  -2)

Решение.

По правилу Лопиталя берем производные числителя и знаменателя и находим предел частного.

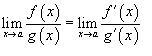
f '(x)=1;  g'(x)=3 / 2√(3x-2)

lim_x->2 f'/g' = lim_x->2 2√(3x-2) /3 = 2√(3*2-2) /3 = 4/3

№ 2.  lim_x→∞ (3x²-4)/(2x²-3x-18)       Делим числитель и знаменатель на х²

lim_x→∞ (3 -4/x²)  / (2 -3/x -18/x²) =  (3 -0) / (2 -0 - 0) = 3/2 = 1,5

№ 3.  Используя правило Лопиталя, найти предел функции

lim _x→∞ x²/ln(e^{x^2}+1)

Решение.    Производная числителя   А=2х

Производная знаменателя  В=(1/(e^{x^2} +1) ) *(e^{x^2}+1)' = 2x*e^{x^2} / (e^{x^2}+1)

Делим произв. числ. на произв. знам. А/В= 2x/(2x*e^{x^2})  *(e^{x^2}+1) = (e^{x^2}+1) / e^{x^2} =  1 + 1/e^{x^2}

lim (1 + 1/e^{x^2}) = 1+0 = 1

x-> ∞

Ответ: 1.

№ 4. lim_x→0 ( arcsinx⁄ sinx) -?

lim_x→0  ( arcsinx)' ⁄ (sinx)' = lim_x→0 (1/√(1-x²) / cosx = 1/cos0 = 1/1 = 1

Ответ: 1.