Строить график надо по схеме:
1. Область определения и точки разрыва функции.
2. Четность и нечетность
3 Периодичность
4. Нули функции
5. Интервалы знакопостоянства
6. Асимптоты **
7. Экстремумы и интервалы монотонности
8. Точки перегиба и интервалы выпуклости и вогнутости графика функции **
9. Область изменения функции
Пункты 6** и 8** необязательны в школьном курсе.
Примеры.
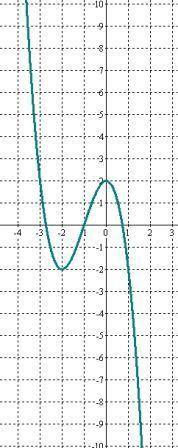
№ 1. Построим график функции у= 2 - 3х2 - х3
- функция непрерывна на (-∞; +∞)
- у'=(2-3x2-x3)' = - 6x - 3x2
- y'=0; -3x(2+x)=0; x1=0, x2=-2 - критические точки.
- 4. y'(x) __ + _ знаки производной
–∞ _______________-2_______________0______________________ +∞
y(x) убывает ↓ возрастает ↑ убывает ↓
x=-2 – точка минимума, х=0 – точка максимума
- у(-2)= 2– 3(-2)2-(-2)3 = -2 минимум функции в точке (-2,-2)
y(0) = 2-0-0=2 максимум функции в точке (0,2)
- Найдем нули функции: 2-3х2-х3=2-2х2-х2-х3=2(1-х2) - х2(1+х) = (1+х)(2-2х-х2) = 0,
т.о. х1=-1, х2=-1-√3 ≈ -2.7, х3=-1+√3 ≈ 0.7 .
Точки х1, х2, х3 - точки пересечения графика функции с осью OX.
- Нанесем на плоскость полученные точки (х1,0); (х2,0), (х3,0) и точки (-2,-2), (0,2), а также используя информацию о промежутках убывания и возрастания, строим график.
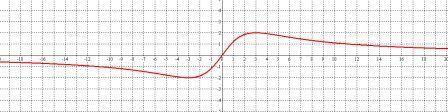
№ 2. Построить график функции y=12x/(9+x2)
функция непрерывна на (-∞; +∞),
нечетная,т.к. у(-х)=-у(х). Поэтому достаточно построить график при х>0, а затем повернуть построенную ветвь на 180° (симметрично отбразить относительно 0).
ноль функции один: у=0 при х=0. (0;0)
решим y'=0, у' = [12(9+x2) - 12x*2x] / (9+x2)2 = 0, приравнивая числитель к 0, получим критические точки: x=±3. Значения функции в критических точках y(3)=2, у(-3)=-2
y'<0 при х>3 (функция убывает), у'>0 при 0<х<3 (фукция возрастает)
Легко видеть, что при х→+∞ функция стремится к 0, оставаясь положительной