Задание ЕГЭ №7. На рисунке изображен график производной функции на интервале
liliana :
Полезная ссылка:
Исследование функций. Нахождение точек максимума, минимума,
наибольшего и наименьшего значений функции
1. На рисунке изображен график производной функции у=f(x).
Требуется определить количество точек экстремума функции у=f(x).
Точки экстремума - это точки минимума и максимума функции f(x). Если производная у=f(x) равна 0 в некоторой точке, то в этой точке экстремум функции, а сама точка - точка экстремума. Смотрим, сколько раз график производной пересекает ось ОХ. На рисунке (ниже) график пересекает ось ОХ 3 раза, значит функция у=f(x) имеет 3 точки экстремума.
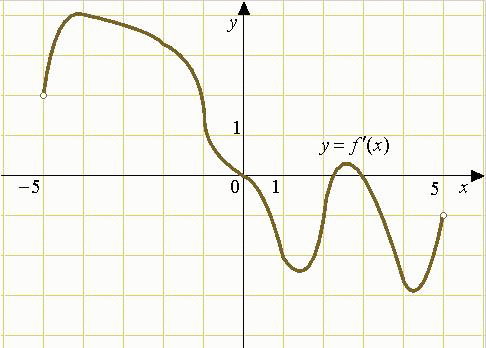
2. На рисунке изображена производная функции у=f(x).
Требуется определить точки минимума и максимума функции f(x).
Определим, в каких точках производная равна 0.
Это точки х=0; х=2,3; х=3.
При переходе через точку х=0 производная меняет знак с плюса на минус. Это значит, что слева от точки х=0 функция f(x) возрастает, а справа от точки х=0 убывает. Значит, в точке х=0 максимум функции. На этом графике мы не можем определить значение максимума функции, а только указать на точку максимума х=0.
Аналогично, х=3 - точка максимума.
х=2,3 - точка минимума, т.к. при переходе через неё производная меняет знак с минуса на плюс.