Геометрическая вероятность. Задачи с решениями.
liliana :
Геометрическая вероятность – вероятность попадания точки в область (отрезок, часть плоскости и т.д.).
1. Пусть отрезок CК лежит на отрезке АВ. На отрезок АВ наудачу поставлена точка. Это означает, что поставленная точка может оказаться в любой точке отрезка АВ, вероятность попадания точки на отрезок СК не зависит от его расположения относительно отрезка АВ и вычисляется по формуле
Р = длина СК / длина АВ.
А________С______К_______________В
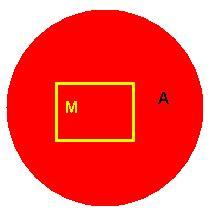
2. Пусть плоская фигура М составляет часть плоской фигуры А.
На фигуру А наудачу брошена точка. Это означает, что брошенная точка может оказаться в любой точке фигуры А. Вероятность попадания брошенной точки на фигуру М не зависит ни от ее расположения относительно А, ни от формы фигуры М. Вероятность попадания точки в фигуру М определяется равенством
Р = Площадь М / Площадь А.